La question de l’agrégation des préférences individuelles fait l’objet de recherches dans plusieurs disciplines, en particulier en économie et dans les sciences de la complexité. Elle est par ailleurs au coeur de tout système démocratique. Dans la plupart des pays du monde, l’agrégation des préférences individuelles se fait en deux temps (au moins) :
- les partis politiques représentent des agrégats de préférences individuelles aux contours plus ou moins bien définis
- le système électoral amène à choisir entre les partis, en général avec un mode de scrutin uninominal majoritaire (France, États-Unis, etc.)
“La méthode Condorcet (ou vote Condorcet) est un système de vote dans lequel l’unique vainqueur est celui, s’il existe, qui, comparé tour à tour à tous les autres candidats, s’avèrerait à chaque fois être le candidat préféré.” (voir la page Wikipedia en français et surtout en anglais). Elle est utilisée dans certains organismes, en particulier dans le monde du logiciel libre (Communauté Debian). Ce candidat idéal, préféré dans tous les duels, n’existe pas forcément : c’est le paradoxe de Condorcet, pour lequel il existe plusieurs méthodes de résolution.
Présentation du problème
Cet exemple est tiré du stage mutualisé des masters Carthagéo et Géoprisme. Les étudiants participant au stage forment 7 groupes de 3 à 4 étudiants chacun et chaque groupe choisit un projet dans une liste de 7 projets (liste en annexe). Dans un tel cas, il y a déjà deux niveaux d’agrégation :
- Chaque individu a un ordre de préférence qui aboutit à l’ordre de préférence du groupe
- Chaque groupe a un ordre de préférence qui aboutit à l’ordre de préférence global
Application
Nous aurons besoin des packages suivants :
library(permute)
library(plyr)
library(reshape2)
Nous avons 7 groupes dont chacun doit choisir parmi 7 projets (liste en annexe). Voici la liste ordonnée des préférences, du projet le plus apprécié au moins aimé:
prefGroup1 <- c(6,1,5,7,3,2,4)
prefGroup2 <- c(1,2,6,3,4,5,7)
prefGroup3 <- c(2,3,5,6,4,1,7)
prefGroup4 <- c(2,6,5,1,3,4,7)
prefGroup5 <- c(3,6,7,1,4,2,5)
prefGroup6 <- c(3,4,7,5,6,1,2)
prefGroup7 <- c(5,6,7,3,2,1,4)
On mets les 7 vecteurs de préférences dans une liste pour pouvoir itérer sur ces vecteurs dans une boucle ou avec des fonctions de type lapply().
listPrefs <- list(prefGroup1, prefGroup2, prefGroup3, prefGroup4, prefGroup5, prefGroup6, prefGroup7)
Classement des projets
Les groupes qui choisissent des projets sont comparables à des individus qui votent pour des candidats. On applique la méthode de Condorcet pour déterminer lequel des projets est le plus aimé. On peut coder la fonction ou bien utiliser une fonction déjà existante. Il existe un package très générique pour le traitement des relations, qui implémente plusieurs méthodes de vote (Condorcet, Borda, etc.) : le package relations. Ici on se contentera de produire la matrice de Condorcet avec les résultats de tous les duels entre projets.
La fonction qui suit crée une liste de liens dirigés selon l’ordre de préférence (respect de la transitivité des préférences : si A > B et B > C alors A > C).
PrepareEdges <- function(vec){
matPref <- matrix(vec, nrow = length(vec), ncol = length(vec), byrow = TRUE)
matPref[lower.tri(matPref, diag = TRUE)] <- NA
matPref <- matPref[- nrow(matPref), ]
tabEdges <- data.frame(X = numeric(), Y = numeric())
for(i in 1:nrow(matPref)){
vec[i]
tempEdges <- expand.grid(X = vec[i], Y = na.omit(matPref[i, ]))
tabEdges <- rbind(tabEdges, tempEdges)
}
return(tabEdges)
}
On applique cette fonction aux 7 vecteurs de préférences stockés plus haut dans la liste listPrefs. Puis on reconstitue le tableau en appliquant une fonction rbind sur tous les résultats de la liste. Finalement, la fonction dcast() permet de créer la matrice de Condorcet. Tout ceci pourrait donner lieu à un traitement sous forme de graphes : dans le vocabulaire de l’analyse de graphes on dira que l’objet tabEdges est une liste d’arcs et l’objet matCondorcet une matrice d’adjacence valuée.
listEdges <- lapply(listPrefs, PrepareEdges)
tabEdges <- do.call(rbind, listEdges)
tabEdges$BIN <- 1
matCondorcet <- dcast(tabEdges, X ~ Y, value.var = "BIN", fun.aggregate = sum)
matCondorcet <- as.matrix(matCondorcet[, -1])
En comparant les lignes et les colonnes on se rend compte de la complexité de l’agrégation des préférences individuelles : par exemple, le projet 1 l’emporte sur le 2 (par 4 votes contre 3), perd contre le projet 3 (par 3 votes contre 4), gagne contre le 4, perd contre le 5, perd contre le 6 et gagne contre le 7. Le projet 3 est clairement plus apprécié que le projet 1, il gagne tous ses duels sauf contre le projet 6. Le projet 6 est le candidat idéal de Condorcet, il gagne tous ses duels.
cbind(matCondorcet[1, ], matCondorcet[, 1])
## [,1] [,2]
## 1 0 0
## 2 4 3
## 3 3 4
## 4 5 2
## 5 3 4
## 6 1 6
## 7 4 3
cbind(matCondorcet[6, ], matCondorcet[, 6])
## [,1] [,2]
## 1 6 1
## 2 4 3
## 3 4 3
## 4 6 1
## 5 4 3
## 6 0 0
## 7 6 1
Assignation optimale des projets
Dans cette section il ne s’agit plus de voir quel est le projet préféré mais de savoir quelle est l’assignation optimale des projets aux groupes. Pour le moment, l’assignation optimale est vaguement définie comme celle qui produit la plus grande satisfaction globale (ce qui est un raisonemment économique typique : voir à la fin de la section).
On crée toutes les permutations possibles entre les 7 projets, soit $n!$ combinaisons possibles ($7654321 = 5040$). La matrice obtenue a 7 colonnes représentant les 7 groupes, chaque ligne représente une assignation possible des projets aux groupes : par exemple la ligne 1 de projPermutations revient à assigner le projet 1 au groupe 1, le projet 2 au groupe 2, etc.
allPermutations <- allPerms(n = 1:7)
projPermutations <- as.matrix(rbind(1:7, allPermutations))
head(projPermutations)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 1 2 3 4 5 6 7
## [2,] 1 2 3 4 5 7 6
## [3,] 1 2 3 4 6 5 7
## [4,] 1 2 3 4 6 7 5
## [5,] 1 2 3 4 7 5 6
## [6,] 1 2 3 4 7 6 5
L’idée est d’appliquer des scores à chaque projet en ordre croissant : si c’est le projet préféré du groupe on lui attribue un 1, si c’est le second on lui attribue 2, etc.
On duplique la matrice et la modifie dans une boucle qui itère sur les colonnes (groupes) : sur le groupe 1 (i=1, colonne 1), on remplace la valeur trouvée dans la colonne avec un dictionnaire de correspondance qui donne la préférence. Par exemple pour le groupe 1 on a :
from = 6 1 5 7 3 2 4to = 1 2 3 4 5 6 7
La fonction mapvalues fera ce recodage : quand elle trouve un 6 elle recode 1, quand elle trouve un 1 elle recode 2, quand elle trouve un 5 elle recode 3, etc.
prefPermutations <- projPermutations
for(i in 1:7){
prefPermutations[, i] <- mapvalues(prefPermutations[, i],
from = listPrefs[[i]],
to = 1:7)
}
On peut considérer que la combinaison optimale est celle qui minimise la somme des scores. Cette somme est bornée entre 7 et 49 : la combinaison dans laquelle chacun des 7 groupes se voit assigner son projet préférer aura une sommme de $7 * 1$ et la combinaison dans laquelle chaque groupe se voit assigner son projet le moins aimé aura une somme de $7 * 7$.
tabPermutations <- data.frame(projPermutations, SOMME = apply(prefPermutations, 1, sum))
hist(tabPermutations$SOMME, col = "firebrick", border = "white")
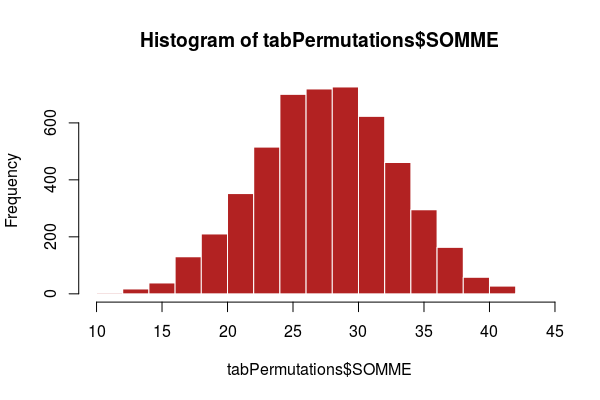
indexMin <- which.min(x = tabPermutations$SOMME)
projPermutations[indexMin, ]
## [1] 6 1 3 2 7 4 5
Conclusion :
- La combinaison optimale est donc la suivante (séquence des numéros de projets) avec une somme de 11 : $6 1 3 2 7 4 5$
- L’arbitrage opéré en classe a donné la combinaison suivante, qui vient juste après, avec une somme de 12 : $6 1 5 2 3 4 7$
Important : le critère utilisé (minimiser la somme) est une fonction utilitariste. Ce n’est pas le seul possible et il traduit l’idée de maximisation du bien commun, au détriment de l’équité par exemple. Si 6 groupes peuvent avoir leur projet préféré grâce au sacrifice d’un seul groupe qui prend le projet détesté, on obtient une somme de 13. Si chacun des 7 groupes obtient son deuxième préféré, on obtient une somme de 14, mais la configuration peut sembler meilleure sur d’autres critères (d’équité).
Annexe : liste des projets
-
Les élus des communes de Midi-Pyrénées veulent limiter l’utilisation de la voiture pour les déplacements sur des courtes distances. Pour favoriser l’utilisation des modes de transports actifs (marche à pied, vélo etc.), ils proposent de mettre en place dans certaines communes “prioritaires” des mesures incitatives (aide à l’achat d’un vélo électrique ou d’un chariot pour transporter les enfants en vélo etc.). Ils demandent alors à une équipe de géographes d’identifier et de décrire les profils des communes dans lesquelles la population utilise prioritairement la voiture pour se rendre au travail alors même que la distance à parcourir depuis le lieu de résidence est réduite. Pour compléter cette analyse, ils veulent également connaitre le profil social et démographique des populations qui utilisent leur voiture pour se rendre au travail.
-
Une association de citoyens de Midi-Pyrénées souhaite disposer d’un état des lieux sur le parc HLM des communes de Toulouse et des environs en lien avec les obligations fixées par la loi SRU (loi SRU puis Duflot : voir le détail des critères). Elle se met en contact avec une équipe de géographes et lui demande de réaliser une cartographie des communes selon leur parc HLM et de décrire le profil géographique, social et démographique des communes dans lesquels la proportion d’HLM est (trop) faible. L’association souhaite également en savoir plus sur les populations qui résident en HLM : elle se demande notamment si les profils sociaux et démographiques des habitants de logements HLM divergent selon les communes.
-
La Mairie de Toulouse souhaite visualiser sur une carte les lignes de “fracture territoriale” qui mettent en contact des quartiers ayant des conditions économiques et sociales radicalement différentes. L’équipe devra à la fois réaliser la commande mais aussi s’interroger sur les motivations du commanditaire.
-
Toulouse Métropole lance un programme de prospective dont l’un des axes consiste à anticiper les futures extensions de l’aire urbaine (définition Insee). L’équipe en charge du projet a pour mission de détecter quelles communes en marge de l’aire urbaine risquent d’être absorbées dans l’aire urbaine toulousaine dans les années qui viennent.
-
La Commission “Logement” de Toulouse Métropole cherche à dresser un panorama sur le thème “Logement et vulnérabilité”. Il s’agit pour l’équipe de proposer des critères de vulnérabilité, de détecter les logements à cibler et d’examiner la pertinence de mettre en place des zones d’action pour lutter contre la vulnérabilité du parc de logements.
-
La Commission “Urbanisme et Transport” de Toulouse Métropole lance une étude sur les effets du zonage fonctionnel dans l’aire urbaine. Il s’agit de dresser un tableau des communes des relations résidents-emplois, de détecter les communes-dortoirs et les zones d’activités, de caractériser les résidents pour les communes-dortoirs et les emplois pour les zones d’activités, et enfin de caractériser les modes de transport utilisés (pour sortir des communes-dortoirs en particulier).
-
L’association “Citoyens du monde” s’inquiète des processus de ségrégation des immigrés et des étrangers, à la fois au lieu d’emploi et au lieu de résidence. Elle cherche à détecter les zones les plus ségrégées et à caractériser le plus finement possible les individus, les logements et les contextes spatiaux de cette ségrégation.